Categories

Sponsors


Archive
 Blogroll 
Badges


Community

|
Posted in Motorlar | No Comment | 4,496 views | 06/02/2009 15:47
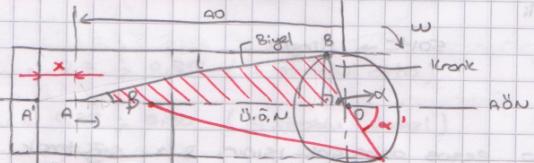
Kafama takılan bir problem bu şuan. Piston yolu hesabı üzerinden teorik olarak nasıl bulunabildiğini biliyoruz. Peki ya gerçek bir motor üzerinde nasıl hesap yapabilirim? Gerçek bir motorun, sıkıştırma prosesi sırasında pistonun üst ölü noktaya olan uzaklığı nasıl hesaplanabilir? Piston hareket ederken, biyel açısı ya da krank mili açısı tespit edilebilir mi? Bu noktada sanırım işin içine konstrüktif tasarım etki ediyor. Biyel boyu hangi proseste olursa olsun sabit olmalı. Krank yarıçapı da zaten sabit. Peki ya krank açısı? Krank açısının her değişimi, bizi farklı sonuçlara götürüyor. Krank yarıçapı R ve Biyel uzunluğu L sabit olmasına rağmen biyel, krank çapı üzerinde hareket ettiği için farklı zamanlarda farklı noktalarda olacak ve bu da pistonun X uzaklığını yani ÜÖN’ya olan uzaklığını arttıracaktır. Bu nedenle, piston üst ölü noktaya vardığında; A’O = L + R
diyebiliriz. Üst ölü nokta konumuna A’, krank mili eksenine de O dedim. Böylece L + R toplamı bize A’O uzaklığı vermeli. Bu noktada zaten X uzaklığı sıfır olacaktır. Yalnız farklı noktalardaki X uzaklığını hesaplamak istersek, bu noktalardaki krank mili açısını tespit etmemiz gerekli. Çünkü ancak bu açı bize doğru sonuca götürür. Peki çalışan motorda, bu açıyı nasıl hesaplayacağız? İşte benim şuanki bilgilerimle veremeyeceğim bir cevap bu. Sanırım motora eklenen elektronik algılayıcılar ile bu açı ölçülebiliyordur. Bu yüzden krank mili açısı olan alfa açısını da bulabildiğimizi varsayarak devam ediyorum. AO = AC + CO
AC’yi bulabilmek için ABC üçgenini kullanalım. Cosβ = AC / L –> AC = L * Cosβ
CO’yu bulabilmek için BCO üçgenini kullanalım. cosα = CO / R –> CO = cosα * R
Buradan X uzaklığına geçiş yaparsak: X = L + R – L * cosβ – R * cosα
= R ( 1 – cosα + L/R ( 1 – cosβ ) Yukarda dönüştürebileceğimiz bir ifade oluştu: R / L = λ
λ oranına biyel oranı denir ve konstrüktif bir faktördür. 0,23 ila 0,3 arasında değişen bir değer alır ve motor tasarlanırken göz önünde tutulur. β’yı α cinsinden ifade etmeye çalışalım; cos2β + sin2β = 1
BCO üçgeninden: BC = R * sinα
ABC üçgeninden: BC = L * sinβ
BC’ler ortak olduğu için iki eşitliği birbirine eşitleyelim. L * sinβ = R * sinα
sinβ = λ * sinα Sin ve Cos eşitliğinden çözüme gidersek; X = R ( 1 – cosα + λ / 2 sin2α )
ifadesine ulaşırız. Yalnız yukardaki eşitliğin sadece krank mili açısının ÜÖN’dan sonra verilmesi durumunda geçerli olduğunu belirteyim. AÖN’dan sonra hesap yapmak istersek, farklı bir formül kullanmamız gerekiyor. α açısı değişeceği için ifademizde biraz değişiyor. Diğer formül çıkartımını size bırakıyorum. Kolay gelsin. |